Question

On a coordinate plane, kite H I J K with diagonals is shown. Point H is at (negative 3, 1), point I is at (negative 3, 4), point J is at (0, 4), and point K is at (2, negative 1). Which statement proves that quadrilateral HIJK is a kite? HI ⊥ IJ, and m∠H = m∠J. IH = IJ = 3 and JK = HK = StartRoot 29 EndRoot, and IH ≠ JK and IJ ≠ HK. IK intersects HJ at the midpoint of HJ at (−1.5, 2.5). The slope of HK = Negative two-fifths and the slope of JK = Negative five-halves.

Answer 1

B. IH = IJ = 3 and JK = HK = StartRoot 29 EndRoot, and IH ≠ JK and IJ ≠ HK.

Explanation:

got it correct on edge. have a good day!

Answer 2

(B)IH = IJ = 3 and
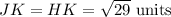`JK = HK = √(29)$ units`, and IH ≠ JK and IJ ≠ HK.

Explanation:

In a kite the following properties applies

Adjacent sides are equal

IH and IJ are adjacent sides

IH=IJ=3 Units

Similarly, JK and HK are adjacent sides and:

`JK = HK = √(29)$ units`

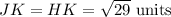
Since opposite sides of a kite must not be equal,

IH ≠ JK and IJ ≠ HK.

Therefore, Option B is the statement that proves that HIJK is a kite.