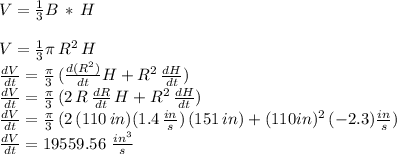Question

The radius of a right circular cone is increasing at a rate of 1.4 in/s while its height is decreasing at a rate of 2.3 in/s. At what rate is the volume of the cone changing when the radius is 110 in. and the height is 151 in.

Answer 1

The volume is changing at a rate given by:

`(dV)/(dt) =19559.56\,\,(in^3)/(s)`

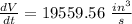
Explanation:

Let's recall the formula for the volume of acone, since it is the rate of the cone changing what we need to answer:

Volume of cone =
`(1)/(3) B\,*\,H`

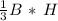
where B is the area of the base (a circle of radius R) which equals =
`\pi\,R^2`

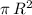
and where H stands for the cone's height.

We apply the derivative over time operator (
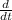`(d)/(dt)`) on both sides of the volume equation, making sure that we apply the rule for the derivative of a product:

`V=(1)/(3) B\,*\,H\\\\V= (1)/(3) \pi\,R^2\,H\\(dV)/(dt) =(\pi)/(3)\,( (d(R^2))/(dt) H+R^2\,(dH)/(dt) )\\(dV)/(dt) =(\pi)/(3)\,( 2\,R\,(dR)/(dt)\, H+R^2\,(dH)/(dt) )\\(dV)/(dt) =(\pi)/(3)\,( 2\,(110\,in)(1.4\,(in)/(s) )\,(151\,in)+(110\.in)^2\,(-2.3)(in)/(s) )\\(dV)/(dt) =19559.56\,\,(in^3)/(s)`