Answer:
Thurka got 8 questions right and 4 wrong.
Explanation:
Thurka got "x" questions right and "y" questions wrong, therefore the sum of these questions must be equal to the total number of questions in that exam, which would be 12, therefore:
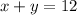
Since for each right question Thurka got 5 marks and for each wrong one 2 marks, then the total score can be written as:
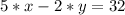
Solving the system of equations would give us the number of right and wrong questions.

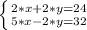
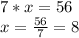

Thurka got 8 questions right and 4 wrong.