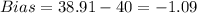Answer:

And replacing we got:
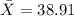
And we can find the bias with this formula:
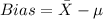
And replacing we got:
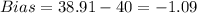
Explanation:
For this problem we know that the random variable of interest follows this distribution:
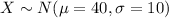
And we have the following random sample given:
39.2, 45.7, 27.4, 25.9, 25.1, 46.3, 42.9, 49.0, 40.6, 47.0
And we can calculate the sample mean with the following formula:

And replacing we got:
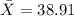
And we can find the bias with this formula:
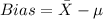
And replacing we got: