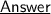
Let's find out the gradient (Slope " m ") of line q ;
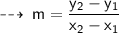
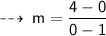
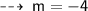
Now, since we already know the gradient let's find of the equation of line by using its Slope and one of the points using point slope form of line :

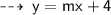
Now, plug in the value of gradient ~
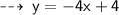
here we can clearly observe that, the Area under the curve can easily be represented as :

Since, all the values of y that lies in the shaded region is smaller than the actual value of y for the corresponding values of x in the equation of line q