Question

A quality control specialist at a pencil manufacturer pulls a random sample of 45 pencils from the assembly line. The pencils have a mean length of

17.9 cm. Given that the population standard deviation is 0.25 cm, find the P-value you would use to test the claim that the population mean of
pencils produced in that factory have a mean length equal to 18.0 cm.​

Answer 1

The P-value you would use to test the claim that the population mean of pencils produced in that factory have a mean length equal to 18.0 cm is 0.00736.

Explanation:

We are given that a quality control specialist at a pencil manufacturer pulls a random sample of 45 pencils from the assembly line.

The pencils have a mean length of 17.9 cm. Given that the population standard deviation is 0.25 cm.

Let
`\mu` = population mean length of pencils produced in that factory.

So, Null Hypothesis,
`H_0` :
`\mu` = 18.0 cm {means that the population mean of pencils produced in that factory have a mean length equal to 18.0 cm}

Alternate Hypothesis,
`H_A` :
`\mu\\eq` 18.0 cm {means that the population mean of pencils produced in that factory have a mean length different from 18.0 cm}

The test statistics that will be used here is One-sample z-test statistics because we know about the population standard deviation;

T.S. =
`(\bar X-\mu)/((\sigma)/(√(n) ) )` ~ N(0,1)

where,
`\bar X` = sample mean length of pencils = 17.9 cm

`\sigma` = population standard deviation = 0.25 cm

n = sample of pencils = 45

So, the test statistics =
`(17.9-18.0)/((0.25)/(√(45) ) )`

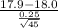
= -2.68

The value of z-test statistics is -2.68.

Now, the P-value of the test statistics is given by;

P-value = P(Z < -2.68) = 1 - P(Z
`\leq` 2.68)

= 1- 0.99632 = 0.00368

For the two-tailed test, the P-value is calculated as = 2
`*` 0.00368 = 0.00736.