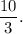Question

M varies directly as n and inversely as the square of p, and

M= 10 when n=8 and p = 2. Find M when n=6 and p = 3.

Answer 1

`(10)/(3).`

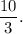
Explanation:

It is given that M varies directly as n and inversely as the square of p. So,

`M\propto (n)/(p^2)`

`M=(kn)/(p^2)`

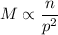
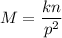
where, k is constant of proportionality.

It is given that M= 10 when n=8 and p = 2.

Substitute M= 10, n=8 and p = 2 in the above equation.

`10=(k8)/(2^2)`

`10=(k8)/(4)`

`10=2k`

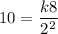
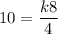
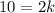
Divide both sides by 2.

`5=k`

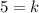
The value of k is 5.

So, requied equation is

`M=(5n)/(p^2)`

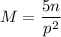
Now, substitute n=6 and p=3 in the above equation.

`M=(5(6))/((3)^2)`

`M=(30)/(9)`

`M=(10)/(3)`

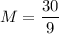
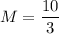
Therefore, the required value of M is
`(10)/(3).`