Question

A consumer is considering two different purchasing options for the car of their choice. The first option, which is leasing, is described by the equation 250x - y + 4000 = 0 where x represents the number of months of ownership and y represents the total paid for the car after ‘x' months. The second option, which is the financing option, will cost $400 for 0 months of ownership, (0,400), and $4400 for 10 months of ownership, (10, 4400). Part A: Find the equations, in slope/y-intercept form, for each of the purchasing options. Explain the significance of the slope and y-intercept for each purchasing option. Part B: Graph each equation on the same set of axes and compare. Under what conditions is each purchasing option the best choice? Be sure to provide a thorough answer. Use detailed information from your graph to back up your choices.

Answer 1

Part A:

First option leasing:

`y = 250x + 4000`

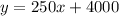
Second option financing:

`y = 400x + 400`

The slope of the second option is greater than the first option meaning that monthly payments are greater for the second option as compared to the first option.

The y-intercept of the first option is greater than the second option meaning that the initial payment of the first option is much greater than the second option.

Part B:

As you can see in the graph, the second option is better when x is less than 24 months and the first option is better when x is greater than 24 months.

The second option has less initial payment but greater monthly payment that is why it is better for the short term (for less number of months)

On the other hand, the first option has a greater initial payment but less monthly payment that is why it is better for the long term (for greater number of months)

Explanation:

Part A:

First option leasing:

The standard slope-intercept form is given by

`y = mx + b`

Convert the given equation into slope-intercept form.

`250x - y + 4000 = 0 \\\\y = 250x + 4000`

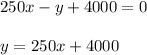
where x represents the number of months of ownership and y represents the total paid for the car after ‘x' months and 250 is the slope that indicates the rate of change of y with respect to x.

Second option financing:

We are given two points,

`(x_1,y_1) = (0,400)`

`(x_2,y_2) = (10,4400)`

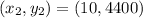
The slope m is given by

`$ m = (y_2 - y_1)/(x_2 - x_1) $`

`$ m = (4400 - 400)/(10 - 0) $`

`m = 400`

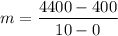
To find the value of the y-intercept (b),

substitute
`(x_1,y_1) = (0,400)`

`y = 400x + b \\\\400 = 400(0) + b \\\\b = 400`

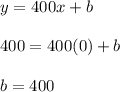
So the equation of the second option is

`y = 400x + 400`

Comparison:

The slope of the second option is greater than the first option meaning that monthly payments are greater for the second option as compared to the first option.

The y-intercept of the first option is greater than the second option meaning that the initial payment of the first option is much greater than the second option.

Part B:

Refer to the attached graph,

The point of intersection is obtained when we equate both equations,

`250x + 4000 = 400x + 400 \\\\4000 - 400 = 400x - 250x \\\\3600 = 150x \\\\x = 3600/150 \\\\x = 24`

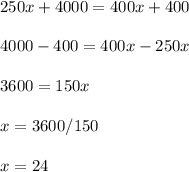
x = 24 months is the break-even point meaning that at this point both options are equally good.

As you can see in the graph, the second option is better when x is less than 24 months and the first option is better when x is greater than 24 months.

The second option has less initial payment but greater monthly payment that is why it is better for the short term (for less number of months)

On the other hand, the first option has a greater initial payment but less monthly payment that is why it is better for the long term (for greater number of months)