Question

A quality control specialist at a pencil manufacturer pulls a random sample of 45 pencils from the assembly line. The pencils have a mean length of

17.9 cm. Given that the population standard deviation is 0.25 cm, find the p-value you would use to test the claim that the population mean of
pencils produced in that factory have a mean length equal to 18.0 cm.​

Answer 1

The p-value you would use to test the claim

p -value = 0.007

Explanation:

Step(i):-

Given random sample size 'n' = 45

Mean of the Population = 18.0 c.m

Standard deviation of the Population(S.D) = 0.25 c.m

Mean of the sample = 17.9 c.m

Null hypothesis :-

H₀ : μ = 18.0 c.m

Alternative Hypothesis:

H₁ : μ ≠ 18.0 c.m

Test statistic

`Z = (x^(-)-mean )/((S.D)/(√(n) ) )`

`Z = (17.9-18 )/((0.25)/(√(45) ) ) = -2.688`

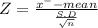
|Z| = |-2.688|

|Z| = 2.688≅ 2.7

Step(ii):-

P -value :-

The z-test statistic value = 2.7

P( Z>2.7) = 1- P(Z< 2.7)

= 1- ( 0.5+ A(2.7))

= 0.5 - A(2.7)

= 0.5 - 0.4965

= 0.0035

P( Z>2.688)= 0.0035

Given data is two tailed test

2 X P( Z>2.688) = 2 X 0.035 = 0.007

P-value = 0.007

we will choose level of significance ∝=0.05

P -value < 0.05

H₀ is rejected

Alternative Hypothesis is accepted

Final answer:-

The population mean of pencils produced in that factory have a mean length is not equal to 18.0 cm.​