Answer:
Option A.
Explanation:
Note: The given function should be
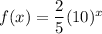 instead of
instead of
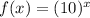 .
.
Consider the given function is
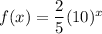
We need to find the function which represents a reflection of f(x) across the x-axis.
If a function f(x) is reflected across the x-axis, then the new function is
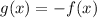
Using this rule, we get
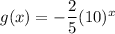
![[\because f(x)=(2)/(5)(10)^x]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/1etv7dtiwue1v0dc6rzviqju0ptirbt3ug.png)
Therefore, the correct option is A.