Question

You have relatives living in the United Kingdom and in France. Suppose that you have purchased a prepaid phone card with a value of $75. Calls to the United Kingdom cost $0.23 per minute, while calls to France cost $0.21 per minute.

(a) Write a linear equation in two variables to represent the number of minutes you can use to call those two locations.
(b) Graph the inequality, and discuss a possible solution in the context of the real-life situation.

Answer 1

a) 0.23x+0.21y=75

b) (For the Graph see the attached picture).

A possible solution for the inequality
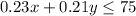`0.23x+0.21y\leq75` would be any point inside the shaded region of the graph. For example (150,175) This is 150 minutes to the United Kingdom and 175 minutes to France.

`0.23x+0.21y\leq75`

`0.23(150)+0.21(175)\leq75`

`34.5+36.75\leq75`

`71.25\leq 75`

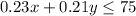
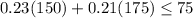
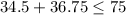
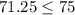
this inequality is true, so the number of minutes used for the United Kingdom and to France is valid.

Explanation:

a)

In order to solve this problem, we must first set our variables:

x= Minutes to the United Kingdom.

y= Minutes to France

The greatest amount of money you can spend is $75 and each minute will cost $0.23 when calling to the United Kingdom and $0.21 when calling to France. So we can use this information to build our equation:

0.23x+0.21y=75.

b) So first, we need to convert our equation into an inequality where the total amount of money spent must be less than $75, so our inequality is:

[tex}0.23x+0.21y\leq75[/tex]

so now we can proceed and graph. This is graphed exactly as you would graph a regular linear equation. You need to find two points on the graph that will satisfy the equation. Plot them and then connect them with a straight line. For example:

First, let's solve the equation for y:

0.23x+0.21y=75

we start by moving the 0.23x to the other side of the equation so we get:

0.21y=-0.23x+75

and next we divide both sides of the equation into 0.21 so we get:

`y=(-0.23x+75)/(0.21)`

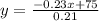
which yields:

y= -1.095x+357.14

next we need to pic an x-value so we can find the first ordered pair. Let's say I pick x=0. So we get:

y= -1.095x+357.14

y= -1.095(0)+357.14

y=357.14

so our first point is (0, 357.14)

And we can follow the same procedure for the second point. Let's say I pick x=1. In that case our second point is (1, 354.04). We can now plot them. Once the graph is drawn, we need to shade it, for which we will pick an ordered pair to the left and an ordered pair to the right of the line. For the left region let's pick the point (0,0) and for the right of the graph, let's pick the point (150,357).

So let's test the inequality for these two points:

First, let's use the point (0,0)

`0.23x+0.21y\leq75`

`0.23(0)+0.21(0)\leq75`

`0\leq75`

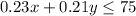
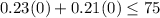
This proves that the left side of the graph is the side to be shaded. We can still use the other point and see what we qet:

(150, 357) and let's use it on our inequality:

`0.23x+0.21y\leq75`

`0.23(150)+0.21(357)\leq75`

`109.47\leq75`

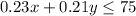
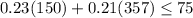
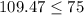
Is a false statement, so only the region on the left will contain the possible number of minutes to do the phone calls to the UK and France.

A possible solution for the inequality
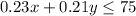`0.23x+0.21y\leq75` would be any point inside the shaded region of the graph. For example (150,175) This is 150 minutes to the United Kingdom and 175 minutes to France.

`0.23x+0.21y\leq75`

`0.23(150)+0.21(175)\leq75`

`34.5+36.75\leq75`

`71.25\leq 75`

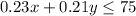
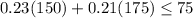
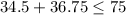
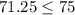
This is a true statement so the possible solution is correct.