Question

g A researcher is interested in whether people are able to identify emotions correctly when they are extremely tired. It is known that, using a particular method of measurement, the accuracy ratings of people in the general population (who are not extremely tired) are normally distributed with a mean of 82 and a variance of 20. In the present study, the researcher arranges to test 50 people who had not slept the previous night. The researcher predicts that these people will have different accuracy than the general population, but does not predict a direction. The mean accuracy for these 50 individuals was a 78. Using the .05 level of significance, what should the researcher conclude

Answer 1

The researcher can conclude that the mean is not 82. i.e. the people will have different accuracy than the general population.

Explanation:

mean,
`\mu = 82`

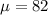
Variance, v = 20

Sample size, n = 50

Standard deviation,
`\sigma = √(20) = 4.4721`

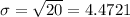
Sample mean,
`\bar{X} = 78`

Level of significance,
`\alpha = 0.05`

Null hypothesis,
`H_o: \mu = 82\\`

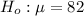
Alternative hypothesis,
`H_a: \mu \\eq 82`

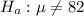
Calculate the test statistics:

`z = \frac{\bar{x} - \mu}{\sigma/√(n) } \\\\z = (78 - 82)/(4.4721√(50) )\\\\z = - 6.32`

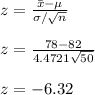
Get the critical value of z at 5% significant level:

`z_(crit) = \pm 1.96`

Since the test statistics is less than the critical values of z, the null hypothesis is rejected.