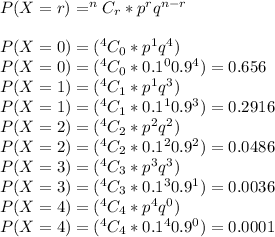Question

Suppose that 10% of all homeowners in an earthquake-prone area of California are insured against earthquake damage. Four homeowners are selected at random. Define the random variable x as the number among the four who have earthquake insurance.

Answer 1

Remainder of question:

Find the probability distribution of x

Answer:

The random variable x is defined as: X = {0, 1, 2, 3, 4}

The probability distribution of X:

P(X = 0) = 0.656

P(X = 1) = 0.2916

P(X= 2) = 0.0486

P(X=3) = 0.0036

P(X = 4) = 0.0001

Explanation:

Sample size, n = 4

Random variable, X = {0, 1, 2, 3, 4}

10% (0.1) of the homeowners are insured against earthquake, p = 0.1

Proportion of homeowners who are not insured against earthquake, q = 1 - 0.1

q = 0.9

Probability distribution of x,

`P(X = r) = ^nC_r *p^r q^(n-r) \\\\P(X= 0) =(^4C_0 *p^1 q^4 )\\P(X=0) = (^4C_0 *0.1^0 0.9^4 ) = 0.656\\P(X= 1)= (^4C_1 *p^1 q^3 )\\P(X=1) = (^4C_1 *0.1^1 0.9^3 ) = 0.2916\\P(X= 2)=( ^4C_2 *p^2 q^2) \\P(X=2) = (^4C_2 *0.1^2 0.9^2 ) = 0.0486\\P(X= 3) = (^4C_3 *p^3 q^3) \\ P(X=3) = (^4C_3 *0.1^3 0.9^1 ) = 0.0036\\P(X= 4) = (^4C_4 *p^4 q^0 )\\ P(X=4) =(^4C_4 *0.1^4 0.9^0 ) = 0.0001`