Question

A particle with a charge of 5 × 10–6 C and a mass of 20 g moves uniformly with a speed of 7 m/s in a circular orbit around a stationary particle with a charge of –5 × 10–6 C. The radius of the orbit is:

Answer 1

r = 0.22m

Step-by-step explanation:

To find the radius of the circular trajectory, you first take into account that the centripetal force of the charged particle, is equal to the electric force between the particle that is moving and the particle at the center of the orbit.

Then, you have:

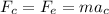`F_c=F_e=ma_c` (1)

m: mass of the particle = 20g = 20*10-3 kg

ac: centripetal acceleration = ?

q: charge of the particle = 5*10^-6C

Fe: electric force between the charges

The electric force is given by:

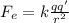`F_e=k(qq')/(r^2)` (2)

r: radius of the orbit

q': charge of the particle at the center of the orbit = -5*10^-6C

Furthermore, the centripetal acceleration is:

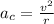`a_c=(v^2)/(r)` (3)

v: speed of the particle = 7m/s

You replace the expressions (2) and (3) in the equation (1) and solve for r:

`k(qq')/(r^2)=m(v^2)/(r)\\\\r=(kqq')/(mv^2)`

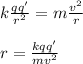
Finally, you replace the values of all parameters in the previous expression:

`r=((8.98*10^9Nm^2/C^2)(5*10^(-6)C)(5*10^(-6)C))/((20*10^(-3)kg)(7m/s)^2)\\\\r=0.22m`

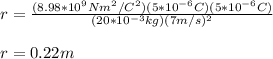
The radius of the circular trajectory is 0.22m