Question

Use the Trapezoidal Rule, the Midpoint Rule, and Simpson's Rule to approximate the given integral with the specified value of n. (Round your answers to six decimal places.)∫414√lnxdx,n=6

Answer 1

• trapezoidal rule: 14.559027
• midpoint rule: 14.587831
• Simpson's rule: 14.577542

Explanation:

We assume you want the integral ...

`\displaystyle\int_4^(14){√(ln(x))}\,dx`

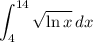
The width of each interval is 1/6 of the difference between the limits, so is ...

interval width = (14 -4)/6 = 10/6 = 5/3

Then the point p[n] at the left end of each interval is ...

p[n] = 4 +(5/3)n

__

Trapezoidal Rule

The area of a trapezoid is the product of its average base length multiplied by the width of the trapezoid. Here, the "bases" are the function values at each end of the interval. The integral according to the trapezoidal rule can be figured as ...

`(5)/(3)\sum\limits_(n=0)^(5)\left((f(p[n])+f(p[n+1]))/(2)\right)`

integral ≈ 14.559027

If you're doing this on a spreadsheet, you can avoid evaluating the function twice at the same point by using a weighted sum. Weights are 1, 2, 2, ..., 2, 1.

__

Midpoint Rule

This rule uses the area of the rectangle whose height is the function value at the midpoint of the interval.

`(5)/(3)\sum\limits_(n=0)^(5){f(p[n+(1)/(2)])}`

integral ≈ 14.587831

__

Simpson's Rule

This rule gives the result of approximating the function over each double-interval by a parabola. It is like the trapezoidal rule in that the sum is a weighted sum of function values. However, the weights are different. Again, multiple evaluations of the function can be avoided by using a weighted sum in a spreadsheet. Weights for 6 intervals are 1, 4, 2, 4, 2, 4, 1. The sum of areas is ...

`(10)/(3)\sum\limits_(n=0)^(2){\left((f(p[2n])+4f(p[2n+1])+f(p[2n+2]))/(6)\right)}`

integral ≈ 14.577542