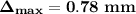Answer:
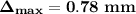
Step-by-step explanation:
From the given information;
A simply supported beam (E = 12 GPa)
load q = 125 N/m
point load P = 200 N
the rectangular cross section
b = 75 mm
h = 200 mm
length = 3.6 m
The objective is to calculate the maximum deflection of the beam;
Using the formula;
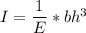 about the z-axis that goes through the central
about the z-axis that goes through the central
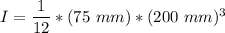

The length L = 3.6 m = 3600 mm
The maximum deflection of the beam can be calculated by using the formula:

![\Delta _(max) = (1)/(12*10^3 (N)/(mm^2)*5*10^7 \ mm^4 )[ (5*(125 \ N)/(100 \ mm)*3600 \ mm^4)/(384)+(200*(3600 \ mm )^3)/(48)]](https://img.qammunity.org/2021/formulas/engineering/college/k3943a9w1hd8okze7a8m32i4rwc21ddecz.png)
Thus; the maximum deflection of the beam is