Answer:
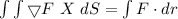 = 12π
= 12π
Explanation:
The field F is given by:
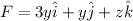 (1)
(1)
The curve C is the ellipse:
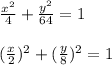
In order to calculate the circulation of F around the curve C, you first find the parametric equation for the given ellipse.
The general form of an ellipse equation is:
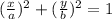
The parametric equation is:
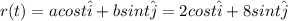 (2)
(2)
The Stokes's theorem is given by the following identity:
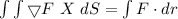
The path integral is also:
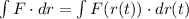 (3)
(3)
For F(r(t)) and dr(t) you obtain:
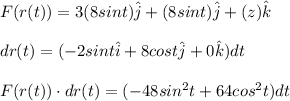
Next, in the equation (3) you obtain:
![\int_0^(2\pi) (-48sin^2t+64cos^2t)dt=\int_0^(2\pi)(-(48)/(2)(1-cos2t)+(64)/(2)(1+cos2t))dt\\\\=\int_0^(2\pi)(-24+24cos2t+32+32cos2t)dt\\\\=\int_0^(2\pi)(6+56cos2t)dt\\\\=[6t+56sin2t]_0^(2\pi)=[6(2\pi)-0]=12\pi](https://img.qammunity.org/2021/formulas/mathematics/college/yknd36tf3qlaktnvawanmwri0bahdoukxt.png)
The circulation of the field around C is 12π