Answer:
the probability of the consumer’s shopping in location 1 is 50.6 %
the probability of the consumer’s shopping in location 2 is 29.9 %
the probability of the consumer’s shopping in location 3 is 19.4 %
Step-by-step explanation:
Huff’s law is a mathematical model that takes consideration in the relation between the patronage and distance from location of the shopping area.
The equation for this mathematical model can be expressed as :

Where;
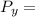 Probability of a consumer travelling from home (i) to shopping location (j)
Probability of a consumer travelling from home (i) to shopping location (j)
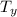 = Travel time from consumer’s home (i) to shopping location (j)
= Travel time from consumer’s home (i) to shopping location (j)
 = Dataset used to determine the effect of travel time in different kinds of shopping trips
= Dataset used to determine the effect of travel time in different kinds of shopping trips
n = Number of different shopping location.
NOW; from the given information.
for location 1 , the consumer shopping probability is :
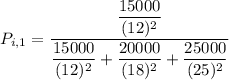
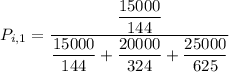


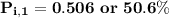
Thus; the probability of the consumer’s shopping in location 1 is 50.6 %
for location 2 , the consumer shopping probability is :
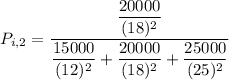
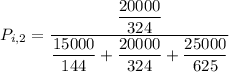
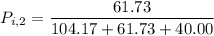

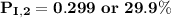
Thus; the probability of the consumer’s shopping in location 2 is 29.9 %
for location 3 , the consumer shopping probability is :

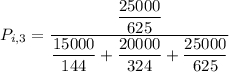
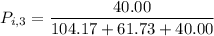
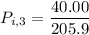
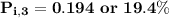
Thus; the probability of the consumer’s shopping in location 3 is 19.4 %