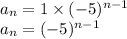Question

Several terms of a sequence StartSet a Subscript n EndSet Subscript n equals 1 Superscript infinity are given below. ​{1​, negative 5​, 25​, negative 125​, 625​, ​...} a. Find the next two terms of the sequence. b. Find a recurrence relation that generates the sequence​ (supply the initial value of the index and the first term of the​ sequence). c. Find an explicit formula for the general nth term of the sequence.

Answer 1

(a) -3125, 15625

(b)

`a_n=-5a_(n-1), \\n\geq 2 \\a_1=1`

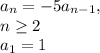
(c)
`a_n=(-5)^(n-1)`

Explanation:

The sequence
`a_n$ _(n=1)^\infty` is given as:

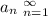`\{1,-5,25,-125,625,\cdots\}`

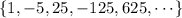
(a)The next two terms of the sequence are:

625 X -5 = - 3125

-3125 X -5 =15625

(b)Recurrence Relation

The recurrence relation that generates the sequence is:

`a_n=-5a_(n-1), \\n\geq 2 \\a_1=1`

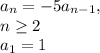
(c)Explicit Formula

The sequence is an alternating geometric sequence where:

• Common Ratio, r=-5
• First Term, a=1

Therefore, an explicit formula for the sequence is:

`a_n=1* (-5)^(n-1)\\a_n=(-5)^(n-1)`