Question

What's the equation of the parabola that has its vertex at (8,–14) and a point (5,13) that lies on the curve?

Question 13 options:

A)

y = (x + 8)2 – 14

B)

y = (x – 8)2 – 14

C)

y = 3(x + 8)2 – 14

D)

y = 3(x – 8)2 – 14

Answer 1

The expression with the described characteristics is:
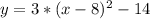`y = 3*(x - 8)^2 - 14`. Therefore the correct answer is letter D.

Explanation:

I believe there is a typo in the vertex's coordinate, I think it should be (8,14). I came to this conclusion by observing the possible answers, if the given vertex is correct then there are no correct answers among them. I made my best effort to explain the question in a way that can be generalized for different vertex's coordinates.

The equations are given in their vertex form. This form has the following structure:

`y = a*(x - h)^2 - k`

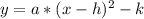
Where (h,k) are the vertex's coordinates, in our case (8, 14). This knowledge makes easier to determine a equation with the correct vertex as shown below:

`y = a*(x - 8)^2 - 14`

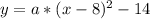
Where the value of "a" must be determined by applying the given point.

`13 = a*(5 - 8)^2 - 14\\13 = a*(3)^2 - 14\\a*9 = 27\\a = (27)/(9)\\a = 3`

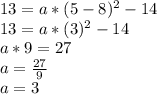
The expression with the described characteristics is:
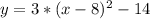`y = 3*(x - 8)^2 - 14`. Therefore the correct answer is letter D.