Question

The length of a rectangle is 5m less than three times the width, and the area of the rectangle is 50m^(2). Find the dimensions of the rectangle

Answer 1

The width is 5m and the length is 10m.

Explanation:

Rectangle:

Has two dimensions: Width(w) and length(l).

It's area is:

`A = w*l`

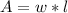
The length of a rectangle is 5m less than three times the width

This means that
`l = 3w - 5`

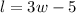
The area of the rectangle is 50m^(2)

This means that
`A = 50`. So

`A = w*l`

`50 = w*(3w - 5)`

`3w^(2) - 5w - 50 = 0`

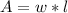
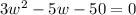
Solving a quadratic equation:

Given a second order polynomial expressed by the following equation:

`ax^(2) + bx + c, a\\eq0`.

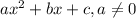This polynomial has roots
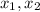`x_(1), x_(2)` such that
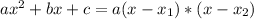`ax^(2) + bx + c = a(x - x_(1))*(x - x_(2))`, given by the following formulas:

`x_(1) = (-b + √(\bigtriangleup))/(2*a)`

`x_(2) = (-b - √(\bigtriangleup))/(2*a)`

`\bigtriangleup = b^(2) - 4ac`

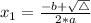
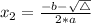
In this question:

`3w^(2) - 5w - 50 = 0`

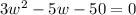
So

`a = 3, b = -5, c = -50`

`\bigtriangleup = (-5)^(2) - 4*3*(-50) = 625`

`w_(1) = (-(-5) + √(625))/(2*3) = 5`

`w_(2) = (-(-5) - √(625))/(2*3) = -3.33`

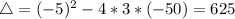
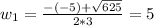
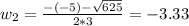
Dimension must be positive result, so

The width is 5m(in meters because the area is in square meters).

Length:

`l = 3w - 5 = 3*5 - 5 = 10`

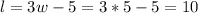
The length is 10 meters