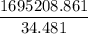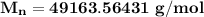Answer:
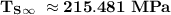
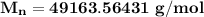
Step-by-step explanation:
The question can be well structured in a table format as illustrated below:
Tensile Strength (MPa) Number- Average Molecular Weight (g/mol)
82 12,700
156 28,500
The tensile strength and number-average molecular weight for two polyethylene materials given above.
Estimate the number-average molecular weight that is required to give a tensile strength required above. Using the data given find TS (infinity) in MPa.
SOLUTION:
We know that :
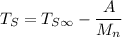
where;
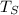 = Tensile Strength
= Tensile Strength
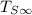 = Tensile Strength (Infinity)
= Tensile Strength (Infinity)
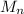 = Number- Average Molecular Weight (g/mol)
= Number- Average Molecular Weight (g/mol)
SO;
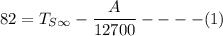
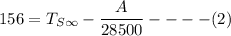
From equation (1) ; collecting the like terms; we have :
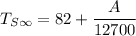
From equation (2) ; we have:
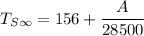
So;
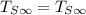
Then;
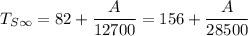
Solving by L.C.M
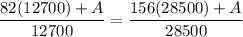
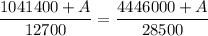
By cross multiplying ; we have:
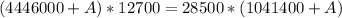
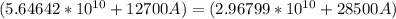
Collecting like terms ; we have
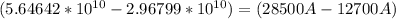
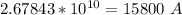
Dividing both sides by 15800:
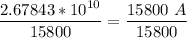
A = 1695208.861
From equation (1);
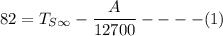
Replacing A = 1695208.861 in the above equation; we have:
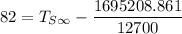
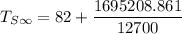
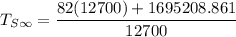
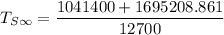
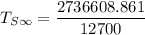
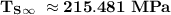
From equation(2);
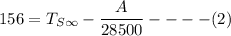
Replacing A = 1695208.861 in the above equation; we have:
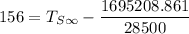
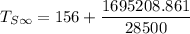
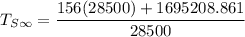
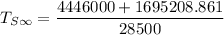
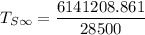
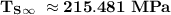
We are to also estimate the number- average molecular weight that is required to give a tensile strength required above.
If the Tensile Strength (MPa) is 82 MPa
Definitely the average molecular weight will be = 12,700 g/mol
If the Tensile Strength (MPa) is 156 MPa
Definitely the average molecular weight will be = 28,500 g/mol
But;
Let us assume that the Tensile Strength (MPa) = 181 MPa for example.
Using the same formula:
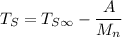
Then:
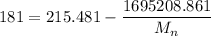
Collecting like terms ; we have:
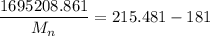
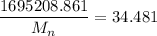
1695208.861= 34.481
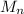
Dividing both sides by 34.481; we have:
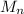 =
=