Question

The time it takes me to wash the dishes is uniformly distributed between 10 minutes and 15 minutes. What is the probability that washing dishes tonight will take me between 12 and 14 minutes

Answer 1

The probability that washing dishes tonight will take me between 12 and 14 minutes is 0.1333.

Explanation:

Let the random variable X represent the time it takes to wash the dishes.

The random variable X is uniformly distributed with parameters a = 10 minutes and b = 15 minutes.

The probability density function of X is as follows:

`f_(X)(x)=(1)/(b-a);\ a<X<b,\ a<b`

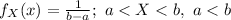
Compute the probability that washing dishes will take between 12 and 14 minutes as follows:

`P(12\leq X\leq 14)=\int\limits^(12)_(14) {(1)/(15-10) \, dx`

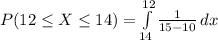
`=(1)/(5)\int\limits^(12)_(14) {1} \, dx \\\\=(1)/(5)* [x]^(14)_(12)\\\\=(1)/(15)* [14-12]\\\\=(2)/(15)\\\\=0.1333`

Thus, the probability that washing dishes tonight will take me between 12 and 14 minutes is 0.1333.