Question

I NEED HELP PLEASE ASAP!!!

Answer 1

see below

Explanation:

There are a couple of ways to go about this.

The general form of a conic equation is ...

Ax^2 +Bxy +Cy^2 +Dx +Ey +F = 0

For AC > 0, this is the equation of an ellipse or circle. (AC < 0, hyperbola; AC = 0, parabola)

So, from the coefficients of the given equation, AC = 2·5 = 10, you know the equation is of an ellipse.

__

The rotation matrix for Cartesian coordinates tells you ...

x = x'·cos(θ) +y'·sin(θ)

y = -x'·sin(θ) +y'·cos(θ)

For θ = 45° the values of these trig functions are all (√2)/2. That is, there is no way to get coefficients in the rotated equation that involve √3. This eliminates choice 2.

The only remaining viable choice is choice 4.

__

If you like, you can substitute for x and y using the above relations. You will find that the result differs from any of the answer choices. The rotated figure will have the equation ...

`5x^2-6xy+9y^2+10√(2)x+2√(2)y-80=0`

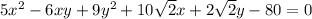
For example, the x and y terms become ...

`6x-4y=6(x'\cos{(45^(\circ))}+y'\sin{(45^(\circ))})-4(-x'\sin{(45^(\circ))}+y'\cos{(45^(\circ))})\\\\=10x'(√(2))/(2)+2y'(√(2))/(2)\\\\\text{Multiplying this by 2 gives $\dots$}\\\\10x'√(2)+2y'√(2)`

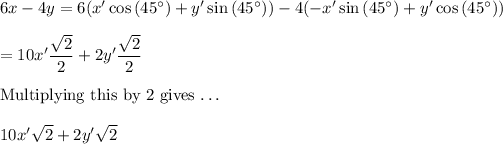
Note that this is not the 10√2x' -10√2y' shown in choice 4.

__

Another way to look at this is to look at the angle of rotation relative to alignment with the x- and y-axes. That angle α is given by ...

cot(2α) = (A -C)/B

For the original ellipse, the rotation angle is ...

α = arccot((2 -5)/2)/2 ≈ -16.85°

For the transformed ellipse of choice 4, the rotation angle is ...

α = arccot((9 -5)/6)/2 ≈ 28.15°

This is 45° more*, as it should be, indicating choice 4 is the better of the offered choices.

__

If you do the angle calculation for the 2nd answer choice, you will find it has no relation to a 45° rotation of the original ellipse.

_____

* While the computed rotation angle is as expected, the fact that the x^2 and y^2 coefficients have been swapped means that the long and short axes of the ellipse have been swapped. That is, the long axis of the ellipse has been rotated 45° in the wrong direction by the equation given in the answer choices. The second attachment shows the original ellipse (red), the properly rotated ellipse (dashed red) and the ellipse of choice 4 (blue).