Answer:
The approximate percentage of women with platelet counts between 127.7 and 378.5
P( 127.7 ≤x≤378.5) = 0.9544 or 95 percentage
Explanation:
Step(i):-
Mean of the Population = 253.1
Given standard deviation of the Population = 62.7
Given sample size 'n' = 873
Let 'X' be the random variable in Normal distribution
Let x₁ = 127.7
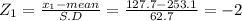
Let x₂ = 378.5
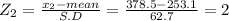
Step(ii):-
The probability of women with platelet counts between 127.7 and 378.5.
P( 127.7 ≤x≤378.5) = P( -2≤Z≤2)
= P(Z≤2) - P(Z≤-2)
= 0.5 +A(2) - ( 0.5 - A(-2))
= A(2) + A(2) (∵A(-2) =A(2)
= 2 × A(2)
= 2× 0.4772
= 0.9544
Conclusion:-
The approximate percentage of women with platelet counts between 127.7 and 378.5 is 0.9544 or 95 percentage