Question

The altitude of a triangle is increasing at a rate of 1.500 centimeters/minute while the area of the triangle is increasing at a rate of 2.000 square centimeters/minute. At what rate is the base of the triangle changing when the altitude is 8.000 centimeters and the area is 98.000 square centimeters?

Answer 1

The base of the triangle is shrinking at a rate of
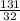`(131)/(32)` centimeters per minute.

Explanation:

The formula of the area of a triangle is given by the following expression:

`A = (1)/(2)\cdot b \cdot h`

Where:

`A` - Area of the triangle, measured in square centimeters.

`b` - Base of the triangle, measured in centimeters.

`h` - Height of the triangle, measured in centimeters.

The base of the triangle is:

`b = (2\cdot A)/(h)`

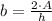
If
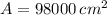`A = 98000\,cm^(2)` and
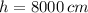`h = 8000\,cm`, the base of the triangle is:

`b = (2\cdot (98000\,cm^(2)))/(8000\,cm)`

`b = 24.5\,cm`

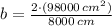
The rate of change of the area of the triangle in time, measured in minutes, is obtained after differentiating by rule of chain and using deriving rules:

`(dA)/(dt) = (1)/(2)\cdot h\cdot (db)/(dt) + (1)/(2)\cdot b \cdot (dh)/(dt)`

`(dA)/(dt) = (1)/(2) \cdot \left(h\cdot (db)/(dt)+b \cdot (dh)/(dt) \right)`

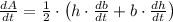
The rate of change of the base of the triangle is now cleared:

`2\cdot (dA)/(dt) = h\cdot (db)/(dt) + b\cdot (dh)/(dt)`

`h\cdot (db)/(dt) = 2\cdot (dA)/(dt)-b\cdot (dh)/(dt)`

`(db)/(dt) = (2\cdot (dA)/(dt) - b \cdot (dh)/(dt) )/(h)`

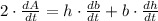
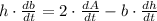
Given that
`(dA)/(dt) = 2000\,(cm^(2))/(min)`,
`b = 24.5\,cm`,
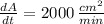`(dh)/(dt) = 1500\,(cm)/(min)` and
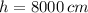`h = 8000\,cm`, the rate of change of the base of the triangle is:

`(db)/(dt) = (2\cdot \left(2000\,(cm^(2))/(min) \right)-(24.5\,cm)\cdot \left(1500\,(cm)/(min) \right))/(8000\,cm)`

`(db)/(dt) = -(131)/(32)\,(cm)/(min)`

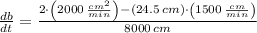
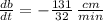
The base of the triangle is shrinking at a rate of
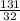`(131)/(32)` centimeters per minute.