Answer:
The base of the triangle is shrinking at a rate of
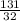 centimeters per minute.
centimeters per minute.
Explanation:
The formula of the area of a triangle is given by the following expression:
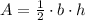
Where:
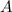 - Area of the triangle, measured in square centimeters.
- Area of the triangle, measured in square centimeters.
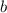 - Base of the triangle, measured in centimeters.
- Base of the triangle, measured in centimeters.
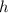 - Height of the triangle, measured in centimeters.
- Height of the triangle, measured in centimeters.
The base of the triangle is:
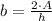
If
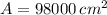 and
and
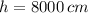 , the base of the triangle is:
, the base of the triangle is:
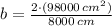
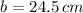
The rate of change of the area of the triangle in time, measured in minutes, is obtained after differentiating by rule of chain and using deriving rules:
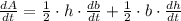
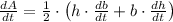
The rate of change of the base of the triangle is now cleared:
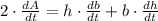
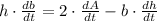
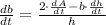
Given that
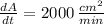 ,
,
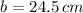 ,
,
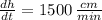 and
and
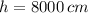 , the rate of change of the base of the triangle is:
, the rate of change of the base of the triangle is:
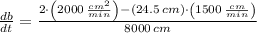
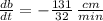
The base of the triangle is shrinking at a rate of
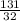 centimeters per minute.
centimeters per minute.