Question

Assume that the readings on the thermometers are normally distributed with a mean of 0 degrees0° and standard deviation of 1.00degrees°C. Assume 2.52.5​% of the thermometers are rejected because they have readings that are too high and another 2.52.5​% are rejected because they have readings that are too low. Draw a sketch and find the two readings that are cutoff values separating the rejected thermometers from the others.

Answer 1

For this question, we assume that 2.5% of the thermometers are rejected at both sides of the distribution because they have readings that are too low or too high.

Answer:

The "two readings that are cutoff values separating the rejected thermometers from the others" are -1.96 Celsius degrees (below which 2.5% of the readings are too low) and 1.96 Celsius degrees (above which 2.5% of the readings are too high).

Explanation:

We can solve this question using the standard normal distribution. This is a normal distribution with mean that equals 0,
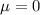`\\ \mu = 0`, and standard deviation that equals 1,
`\\ \sigma = 1`.

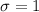And because of using the standard normal distribution, we are going to take into account the following relevant concepts:

• Standardized scores or z-scores, which we can consider as the distance from the mean in standard deviations units, and the formula for them is as follows:

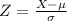`\\ Z = (X - \mu)/(\sigma)` [1]

A positive value indicates that the possible raw value X is above
`\\ \mu`, and a negative that the possible raw value X is below the mean.

• The [cumulative] standard normal table: there exists a table where all these values correspond to a probability, and we can apply it for every possible normally distributed data as well as we first standardize the possible raw values for X using [1]. This table is called the standard normal table, and it is available in all Statistics books or on the Internet.

From the question, we have the following information about the readings on the thermometers, which is a normally distributed random variable:

• Its mean,
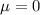  `\\ \mu = 0` Celsius degrees.
• Its standard deviation,
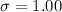  `\\ \sigma = 1.00` Celsius degrees.

It coincides with the parameters of the standard normal distribution, and we can find probabilities accordingly.

It is important to mention that the readings that are too low or too high in the normal distribution are at both extremes of it, one of them with values below the mean,
`\\ \mu`, and the other with values above it.

In this case, we need to find:

• First, the value below which is 2.5% of the lowest values of the distribution, and

• Second, the value above which is 2.5% of the highest values of the distribution.

Here, we can take advantage of the symmetry of the normal or Gaussian distributions. In this case, the value for the 2.5% of the lowest and highest values is the same in absolute value, but one is negative (that one below the mean,
`\\ \mu`) and the other is positive (that above the mean).

Solving the Question

The value below (and above) which are the 2.5% of the lowest (the highest) values of the distribution

Because
`\\ \mu = 0` and
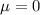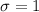`\\ \sigma = 1` (and the reasons above explained), we need to find a z-score with a corresponding probability of 2.5% or 0.025.

As we know that this value is below
`\\ \mu`, it is negative (the z-score is negative). Then, we can consult the standard normal table and find the probability 0.025 that corresponds to this specific z-score.

For this, we first find the probability of 0.025 and then look at the first row and the first column of the table, and these values are (-0.06, -1.9), respectively. Therefore, the value for the z-score = -1.96,
`\\ z = -1.96`.

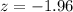As we said before, the distribution in the question has
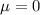`\\ \mu = 0` and
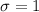`\\ \sigma = 1`, the same than the standard normal distribution (of course the units are in Celsius degrees in our case).

Thus, one of the cutoff value that separates the rejected thermometers is -1.96 Celsius degrees for that 2.5% of the thermometers rejected because they have readings that are too low.

And because of the symmetry of the normal distribution, z = 1.96 is the other cutoff value, that is, the other lecture is 1.96 Celsius degrees, but in this case for that 2.5% of the thermometers rejected because they have readings that are too high. That is, in the standard normal distribution, above z = 1.96, the probability is 0.025 or
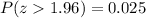`\\ P(z>1.96) = 0.025` because
`\\ P(z<1.96) = 0.975`.

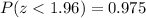Remember that

`\\ P(z>1.96) + P(z<1.96) = 1`

`\\ P(z>1.96) = 1 - P(z<1.96)`

`\\ P(z>1.96) = 1 - 0.975`

`\\ P(z>1.96) = 0.025`

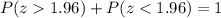
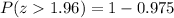
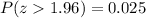
Therefore, the "two readings that are cutoff values separating the rejected thermometers from the others" are -1.96 Celsius degrees and 1.96 Celsius degrees.

The below graph shows the areas that correspond to the values below -1.96 Celsius degrees (red) (2.5% or 0.025) and the values above 1.96 Celsius degrees (blue) (2.5% or 0.025).