Question

The defect length of a corrosion defect in a pressurized steel pipe is normally distributed with mean value 30 mm and standard deviation 7.8 mm [suggested in the article "Reliability Evaluation of Corroding Pipelines Considering Multiple Failure Modes and Time-Dependent Internal Pressure" (J. of Infrastructure Systems, 2011: 216–224)].

What values separate the largest 80% from the smallest 20% of the defect length distribution.

Answer 1

`z=-0.842<(a-30)/(7.8)`

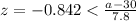
And if we solve for a we got

`a=30 -0.842*7.8=23.432`

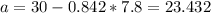
So the value of height that separates the bottom 20% of data from the top 80% is 23.432.

Explanation:

Let X the random variable that represent the heights of a population, and for this case we know the distribution for X is given by:

`X \sim N(30,7.8)`

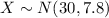
Where
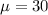`\mu=30` and
`\sigma=7.8`

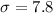
For this part we want to find a value a, such that we satisfy this condition:

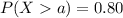`P(X>a)=0.80` (a)

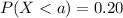`P(X<a)=0.20` (b)

As we can see on the figure attached the z value that satisfy the condition with 0.20 of the area on the left and 0.80 of the area on the right it's z=-0.842

If we use condition (b) from previous we have this:

`P(X<a)=P((X-\mu)/(\sigma)<(a-\mu)/(\sigma))=0.20`

`P(z<(a-\mu)/(\sigma))=0.20`

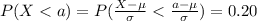
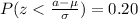
But we know which value of z satisfy the previous equation so then we can do this:

`z=-0.842<(a-30)/(7.8)`

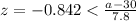
And if we solve for a we got

`a=30 -0.842*7.8=23.432`

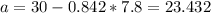
So the value of height that separates the bottom 20% of data from the top 80% is 23.432.