Answer: The area is about 15.59 and is round to the nearest hundredth.
Explanation:
An equilateral triangle has three equal sides is just like an isosceles triangle.
So in this case, we know that the base is 6 and since the base is 6 all the other two sides is also 6 .But we do not know the height to find the area so we need to find the height.
The height is the distance of from the base to the tip or top which helps form two right triangles.. And if you divide as an equilateral triangle into two parts you will form two right triangles. Imagine we have divide the isosceles triangle into two parts to form two right triangles. We will now have a base of 3 instead of 6 and and hypotenuse of 6 . but we still don't know the height so we need to find it.
Using the Pythagorean Theorem we could say that a^2 plus b^2 squared is equal to c^2 squared.
We know a as 3 and c the hypotenuse as 6.
so 3^2 + b^2 =6^2 solve for b
9 + b^2 = 36
-9 -9
b^2 = 27
b=
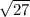
b= 5.196
Now we know that b is about 5.196 which is the height.Now we could find the area by multiplying the base by the height.
5.196 * 6 = 31.176
31.176/2 = 15.588
Now you could round it to the nearest hundredth to be 15.59