Question

The basic function of a carburetor of an automobile is to atomize the gasoline and mix it with air to promote rapid combustion. As an example, assume that 30 cm3 of gasoline is atomized into N spherical droplets, each with a radius of 2.0 × 10−5 m. What is the total surface area of these N spherical droplets? Answer: [A] m2.

Answer 1

The total surface area of these N spherical droplets is 4.4929 m²

Step-by-step explanation:

From the information given :

assuming that :

30 cm³ of gasoline is atomized into N spherical droplets &

each with a radius of 2.0 × 10−5 m

We are tasked to determine the total surface area of these N spherical droplets

We all known that:

`1 \ cm^3 = 10 ^(-6) m^3`

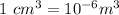
Therefore

`30 \ cm^3 = 30 * 10 ^(-6) m^3 = 3 *1 0^(-5) \ m^3`

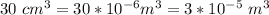
For each droplet; there is a required volume which is =
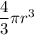`(4)/(3) \pi r ^3` since it assumes a sphere shape .

Thus;

replacing radius(r) with 2.0 × 10−5 m; we have:

`= (4)/(3) \pi * (2.0 *10^(-5) m) ^3`

=
`3.35 * 10^(-14) \ m^3`

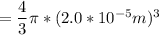
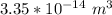
However; there are
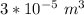`3*10^(-5) \ m^3` gasoline atomized into N spherical droplets with each with radius 2.0 × 10−5 m

For N ; we have ;

`=(3*10^(-5) \ m^3)/(3.35 * 10^(-14) \ m^3/ droplet)`

=
`8.95*10^8 \ droplet s`

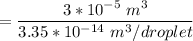
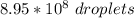
So; each droplet have a surface area =
`4 \pi r^2`

=
`4 \pi (2.0*10^(-5)m) ^2`

=
`5.02*10^(-9) \ m^2/droplets`

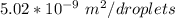
The surface area per droplet is equivalent to
`5.02*10^(-9) \ m^2/droplets`

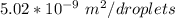
Thus;

The total surface area of these N spherical droplets will be :

=
`8.95*10^8 \ droplet s * 5.02*10^(-9) \ m^2/ droplets`

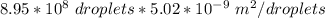
= 4.4929 m²

The total surface area of these N spherical droplets is 4.4929 m²