Answer:
It takes approximately
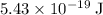 of energy to break one
of energy to break one
 single bond.
single bond.
The maximum wavelength of a photon that can break one such bond is approximately
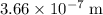 (in vacuum.) That's the same as
(in vacuum.) That's the same as
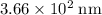 (rounded to three significant figures.)
(rounded to three significant figures.)
Step-by-step explanation:
Energy per bond
The standard bond enthalpy of
 single bonds is approximately
single bonds is approximately
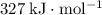 (note that the exact value can varies across sources.) In other words, it would take approximately
(note that the exact value can varies across sources.) In other words, it would take approximately
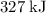 of energy to break one mole of these bonds.
of energy to break one mole of these bonds.
The Avogadro Constant
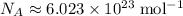 gives the number of
gives the number of
 bonds in one mole of these bonds. Based on these information, calculate the energy of one such bond:
bonds in one mole of these bonds. Based on these information, calculate the energy of one such bond:
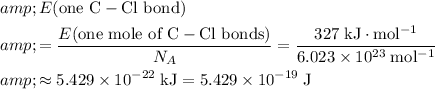 .
.
Therefore, it would take approximately
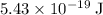 of energy to break one
of energy to break one
 single bond.
single bond.
Minimum frequency and maximum wavelength
The Einstein-Planck Relation relates the frequency
 of a photon to its energy
of a photon to its energy
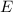 :
:
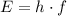 .
.
The
 here represents the Planck Constant:
here represents the Planck Constant:
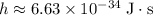 .
.
A photon that can break one
 single bond should have more than
single bond should have more than
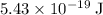 of energy. Apply the Einstein-Planck Relation to find the frequency of a photon with exactly that much energy:
of energy. Apply the Einstein-Planck Relation to find the frequency of a photon with exactly that much energy:
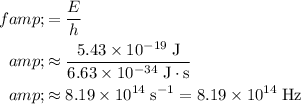 .
.
What would be the wavelength
 of a photon with a frequency of approximately
of a photon with a frequency of approximately
 ? The exact answer to that depends on the medium that this photon is travelling through. To be precise, the exact answer depends on the speed of light in that medium:
? The exact answer to that depends on the medium that this photon is travelling through. To be precise, the exact answer depends on the speed of light in that medium:
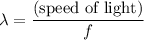 .
.
In vacuum, the speed of light is
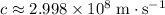 . Therefore, the wavelength of that
. Therefore, the wavelength of that
 photon in vacuum would be:
photon in vacuum would be:
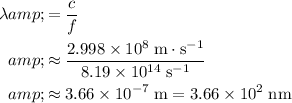 .
.
(Side note: that wavelength corresponds to a photon in the ultraviolet region of the electromagnetic spectrum.)