Question

A simple random sample of 25 items from a normally distributed population resulted in a sample mean of 28 and a standard deviation of 7.5. Construct a 95% confidence interval for the population mean.

Answer 1

CI = 28 ± 3.09

Explanation:

The sample size, n = 25

The sample mean, m = 28

Standard deviation, s = 7.5

Confidence interval is given as:

CI = Sample mean ± margin of error

We want to find 95% confidence level:

First, let us find the margin of error:

Margin of error = Critical value * standard error

To find the critical value, we need some parameters:

Standard error =
`s / √(n)`

=>
`SE = 7.5 / √(25)= 7.5 = 5 = 1.5`

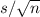
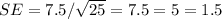
The alpha value, ∝ = 1 - (confidence level / 100) = 1 - 95/100 = 1 - 0.95 = 0.05

Critical probability, p, is given as:

p = 1 - ∝/2 = 1 - 0.05/2 = 1 - 0.025 = 0.975

Now we need the degree of freedom:

df = n - 1 = 25 - 1 = 24

Therefore, the critical value is 2.06 (you can use an online t value calculator).

=> Margin of error = 2.06 * 1.5 = 3.09

Therefore, the confidence interval for the population mean is:

CI = 28 ± 3.09