Question

"Filipe" was playing with a triangle on a coordinate plane. The triangle's area is 242424 square units. The largest circle he can fit in the triangle is centered at (0,0)(0,0)left parenthesis, 0, comma, 0, right parenthesis and passes through the point (1.2,1.6)(1.2,1.6)left parenthesis, 1, point, 2, comma, 1, point, 6, right parenthesis. Approximately what percentage of the triangle does the circle cover?

Answer 1

52%

Explanation:

Khan Academy.

Answer 2

52.33% is the correct answer.

Explanation:

Given that:

Area of triangle = 24 sq units

Center of Circle is at (0, 0) and the circle passes through (1.2, 1.6).

To find: The percentage of triangle covered by circle.

Solution: To find the required percentage, we need to find the area of circle.

To find the area of circle, we need the radius of circle.

Radius of circle is the distance between the center of circle and any point that lies on the periphery of the circle.

We can use Distance formula :

`D = √((x_2-x_1)^2+(y_2-y_1)^2)`

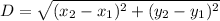
Radius =
`√((1.2-0)^2+(1.6-0)^2) = √(1.44+2.56) = √(4) = 2\ units`

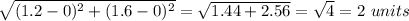
Now, area of circle is given by the formula:

Area =
`\pi r^(2)`

Area = 3.14
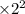`* 2^(2)` = 12.56 sq units

Percentage of Triangle covered:

`(Area\ of\ circle)/(Area\ of\ triangle)* 100\\\Rightarrow (12.56)/(24)* 100\\\Rightarrow 52.33\%`

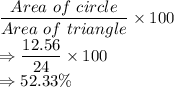
Hence, 52.33% is the correct answer.