Question

Find the area of the polygon XYZ that has its vertices at X(–3, 6), Y(–3, 1), and Z(5,1). Question 8 options: A) 26 square units B) 20 square units C) 40 square units D) 6.5 square units

Answer 1

Area ≈ 20 square units

Explanation:

Using Distance Formula to Find the lengths

Distance Formula =
`√((x2-x1)^2+(y2-y1)^2)`

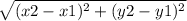
Length XY:

=>
`√((-3+3)^2+(1-6)^2)`

=>
`√(25)`

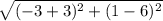
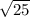
=> 5 units

Length YZ:

=>
`√((5+3)^2+(1-1)^2)`

=>
`√(64)`

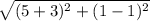
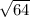
=> 8 units

Length ZX:

=>
`√((-3-5)^2+(6-1)^2)`

=>
`√(89)`

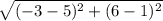
=> 9.4

Perimeter:

=> 5+8+9.4

=> 22.4

Semi-Perimeter:

=> 11.2

Using Heron's Formula to find the area:

Area =
`√(s(s-a)(s-b)(s-c))`

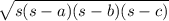
Where s is semi perimeter and a,b and c are side lengths

=> Area =
`√(11.2(11.2-5)(11.2-8)(11.2-9.4))`

=> Area =
`√((11.2)(6.2)(3.2)(1.8))`

=> Area =
`√(399.9)`

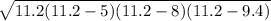
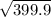
=> Area = 19.99

=> Area ≈ 20 square units