Question

The life of light bulbs is distributed normally. The standard deviation of the lifetime is 25 hours and the mean lifetime of a bulb is 510 hours. Find the probability of a bulb lasting for at most 552 hours.

Answer 1

The probability of a bulb lasting for at most 552 hours.

P(x>552) = 0.0515

Explanation:

Step(i):-

Given mean of the life time of a bulb = 510 hours

Standard deviation of the lifetime of a bulb = 25 hours

Let 'X' be the random variable in normal distribution

Let 'x' = 552

`Z = (x-mean)/(S.D) = (552-510)/(25) =1.628`

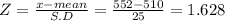
Step(ii):-

The probability of a bulb lasting for at most 552 hours.

P(x>552) = P(Z>1.63)

= 1- P( Z< 1.63)

= 1 - ( 0.5 + A(1.63)

= 1- 0.5 - A(1.63)

= 0.5 -A(1.63)

= 0.5 -0.4485

= 0.0515

Conclusion:-

The probability of a bulb lasting for at most 552 hours.

P(x>552) = 0.0515