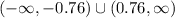Answer:
Explanation:
The first step to solve this question is finding the critical points of the function F(x), which are x for which:
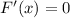
In this question:

So
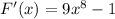
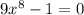
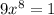
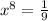
![x = \sqrt[8]{(1)/(9)}](https://img.qammunity.org/2021/formulas/mathematics/college/nm8zgpgqbzmlzj1o4nl3hy0aone60trh9y.png)
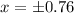
So we have three intervals:
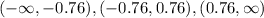
We take a value of x from each interval. If the derivative is positive, the function increases. Otherwise, it decreases.
First interval:

Will take x = -1.
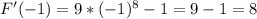
Positive, so increases.
Second interval:
(-0.76, 0.76),
Will take x = 0;
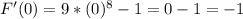
Negative, so decreases
Third interval:

Will take x = 1
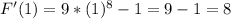
Positive, so increases.
Interval of increase:
First and third, so: