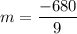Question

Slope of line passes through (7/20, 8/3) and (3/8, 7/9)

Answer 1

`slope = (-680)/(9)`

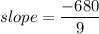
Explanation:

We are given coordinates of two points:

Let the points be A and B respectively:

`A((7)/(20), (8)/(3))\\B((3)/(8), (7)/(9))`

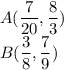
To find the slope of line AB.

Formula for slope of a line passing through two points with coordinates
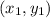`(x_1, y_1)` and
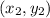`(x_2,y_2)` is given as:

`m = (y_2- y_1)/(x_2- x_1)`

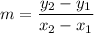
Here, we have:

`x_2 = (3)/(8)\\x_1 = (7)/(20)\\y_2 = (7)/(9)\\y_1 = (8)/(3)\\`

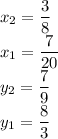
Putting the values in formula:

`m = ((7)/(9)- (8)/(3))/((3)/(8)- (7)/(20))\\\Rightarrow m = ((7-24)/(9))/((15-14)/(40))\\\Rightarrow m = ((-17)/(9))/((1)/(40))\\\Rightarrow m = (-17* 40)/(9)\\\Rightarrow m = (-680)/(9)`

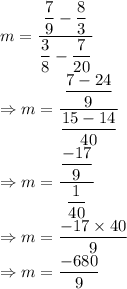
So, the slope of line AB passing through the given coordinates is:

`m = (-680)/(9)`