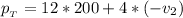Answer:
The total momentum is

Step-by-step explanation:
The diagram illustration this system is shown on the first uploaded image (From physics animation)
From the question we are told that
The mass of the first object is
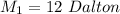
The speed of the first mass is

The mass of the second object is
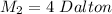
The speed of the second object is assumed to be
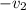
The total momentum of the system is the combined momentum of both object which is mathematically represented as

substituting values