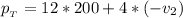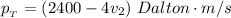Question

The mass of M1 = 12 Daltons and it has a speed of v1 = 200 m/s. The mass of M2 = 4 Daltons. What was the total momentum of the system consisting of both masses before the collision (in Dalton meters per second, assume positive to the right and negative to the left)?

Answer 1

The total momentum is
`p__(T )} =(2400 -4 v_2) \ Dalton \cdot m/s`

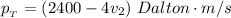
Step-by-step explanation:

The diagram illustration this system is shown on the first uploaded image (From physics animation)

From the question we are told that

The mass of the first object is
`M_1 = 12 \ Dalton`

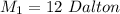
The speed of the first mass is
`v_1 = 200 \ m/s`

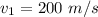
The mass of the second object is
`M_2 = 4 \ Dalton`

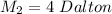
The speed of the second object is assumed to be
`- v_2`

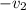
The total momentum of the system is the combined momentum of both object which is mathematically represented as

`p__(T )} = M_1 v_1 + M_2 v_2`

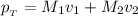
substituting values

`p__(T )} = 12 * 200 + 4 * (-v_2)`

`p__(T )} =(2400 -4 v_2) \ Dalton \cdot m/s`