Question

Assume that we want to construct a confidence interval. Do one of the​ following, as​ appropriate: (a) find the critical value t Subscript alpha divided by 2​,​(b) find the critical value z Subscript alpha divided by 2​,or​ (c) state that neither the normal distribution nor the t distribution applies.Here are summary statistics for randomly selected weights of newborn​ girls: nequals235​,x overbarequals33.7​hg, sequals7.3hg. The confidence level is 95​%.

Answer 1

To construct a confidence interval, Normal distribution should be used since the sample size is quite large (n > 30)

From the z-table, at α = 0.025 the critical value is

`z_(\alpha/2) = 1.96`

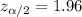
Explanation:

We are given the following information:

The sample size is

`n = 235`

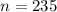
The mean weight is

`\bar{x}= 33.7 \: hg`

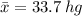
The standard deviation is

`s = 7.3 \: hg`

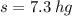
Since the sample size is quite large (n > 30) then according to the central limit theorem the sampling distribution of the sample mean will be approximately normal, therefore, we can use the Normal distribution for this problem.

The correct option is (b)

The critical value corresponding to 95% confidence level is given by

Significance level = α = 1 - 0.95 = 0.05/2 = 0.025

From the z-table, at α = 0.025 the critical value is

`z_(\alpha/2) = 1.96`

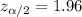
What is Normal Distribution?

A Normal Distribution is a continuous probability distribution and is symmetrical around the mean. The shape of this distribution is like a bell curve and most of the data is clustered around the mean. The area under this bell shaped curve represents the probability.