Question

If we increase the resistance in an RL circuit, what happens to the time required for the current to reach, say, 50% of its final value after the battery is connected?

Answer 1

t = 0.69R/L

If the resistance R increases, the required time decreases, for the battery reaches a 50% of its initial value.

Step-by-step explanation:

In order to know what happens to the the time, when the battery reaches a 50% of its initial voltage, while the RL resistance increases, you use the following formula:

`V=V_oe^{-(R)/(L)t}` (1)

Vo: initial voltage in the battery

V: final voltage in the battery = 0.5Vo

R: resistance of the RL circuit

L: inductance of the RL circuit

You use properties of logarithms to solve the equation (1) for t:

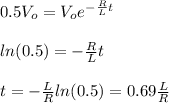`0.5V_o=V_oe^{-(R)/(L)t}\\\\ln(0.5)=-(R)/(L)t\\\\t=-(L)/(R)ln(0.5)=0.69(L)/(R)` (2)

By the result obtained in the equation (2), you can observe that if the resistance R increases, the required time decreases, for the battery reaches a 50% of its initial value.