Answer:
The height of the tower is 23.786 m
Step-by-step explanation:
Given;
period of oscillation, t = 9.79 s
acceleration of gravity, g = 9.8 m/s²
The period of oscillation is calculated as follows;
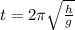
where;
h represents the height of the tower
g is the acceleration of gravity
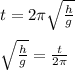
square both sides of the equation;

Therefore, the height of the tower is 23.786 m