Question

In a test of the effectiveness of garlic for lowering​ cholesterol, 4545 subjects were treated with garlic in a processed tablet form. Cholesterol levels were measured before and after the treatment. The changes ​(beforeminus−​after) in their levels of LDL cholesterol​ (in mg/dL) have a mean of 5.15.1 and a standard deviation of 19.119.1. Construct a 9090​% confidence interval estimate of the mean net change in LDL cholesterol after the garlic treatment. What does the confidence interval suggest about the effectiveness of garlic in reducing LDL​ cholesterol?

Answer 1

`5.1 - 2.015 (19.1)/(√(45))= -0.637`

`5.1 + 2.015 (19.1)/(√(45))= 10.837`

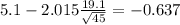
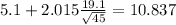
And for this case since the confidence interval contains the value 0 we don't have significant evidence that we have a net change in the levels

Explanation:

For this case we have the following info given:

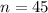`n=45` represent the sample size

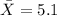`\bar X= 5.1` represent the sample mean

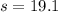`s= 19.1` represent the sample deviation

We can calculate the confidence interval for the mean with the following formula:

`\bar X \pm t_(\alpha/2) (s)/(√(n))`

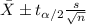
The confidence level is 0.90 then the significance level would be
`\alpha=0.1` and the degrees of freedom are given by:

`df= n-1 = 45-1=44`

And the critical value for this case would be:

`t_(\alpha/2)=2.015`

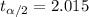
And replacing we got:

`5.1 - 2.015 (19.1)/(√(45))= -0.637`

`5.1 + 2.015 (19.1)/(√(45))= 10.837`

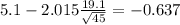
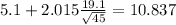
And for this case since the confidence interval contains the value 0 we don't have significant evidence that we have a net change or efectiveness in the levels