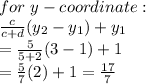Question

Which shows how to find the y-coordinate of the point that will divide CD into a 5:2 ratio using the formula y = (y2 – y1) + y1? y = (3 – 1) + 1 y = (3 + 4) – 4 y = (3 – 1) + 1 y = (3 + 4) – 4

Answer 1

{5/7}(3-1)+1

Explanation:

Answer 2

`(5)/(5+2)(3-1)+ 1`

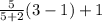
Explanation:

To find the coordinate of the point that divides a line segment AB with point A at (
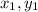`x_1,y_1`) and point B at
`(x_2,y_2)` in the proportion c:d, the formula used to find the location of the point is:

`x-coordinate:\\(c)/(c+d)(x_2-x_1)+x_1 \\\\While \ for\ y-coordinate:\\(c)/(c+d)(y_2-y_1)+y_1`

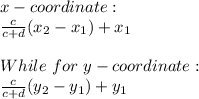
Therefore the y coordinate that divides line segment CD with point C at (
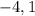`-4,1`) and point D at
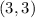`(3,3)` in the proportion 5:2 is given by:

`for\ y-coordinate:\\(c)/(c+d)(y_2-y_1)+y_1\\=(5)/(5+2)(3-1)+ 1\\=(5)/(7)(2)+1=(17)/(7)`