Answer:
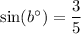 .
.
Explanation:
It is given that,
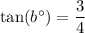
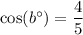
If a figure is dilated, then the image is similar to the figure. It means the corresponding angles of figure and image are congruent.
So, the value of sin(b°) after dilation is equal to the value of sin(b°) before dilation.
We know that,
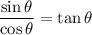
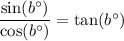
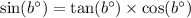
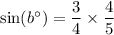
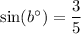
Therefore,
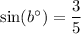 .
.