Question

There are only green pens and red pens in the box.There are three more red pens than green pens in the box.Sheila is going to take at random two pens from the box.The probability that sheila will take two pens of the same colour is 17/35.Work out the two different numbers of green pens that could be in the box.

Answer 1

6 or 9

Explanation:

Let the number of green pens =x

There are three more red pens, therefore:

The number of red pens =x+3

Total Number of pens =x+x+3=2x+3

The probability that sheila will take two pens of the same color =
`(17)/(35)`

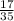
Therefore, we have that:

`\text{P(two red pens)}=(x+3)/(2x+3) * (x+2)/(2x+2)\\\\P(RR)=((x+3)(x+2))/((2x+3)(2x+2))`

`P$(two green pens$)=(x)/(2x+3) * (x-1)/(2x+2)\\\\P(GG)=(x(x-1))/((2x+3)(2x+2))`

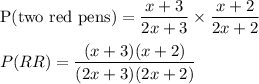
Therefore, the probability that sheila will take two pens of the same color

=P(RR)+P(GG)

`((x+3)(x+2))/((2x+3)(2x+2))+(x(x-1))/((2x+3)(2x+2))=(17)/(35)\\((x+3)(x+2)+x(x-1))/((2x+3)(2x+2))=(17)/(35)\\`

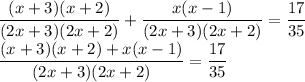
Cross multiply

`35[(x+3)(x+2)+x(x-1)]=17[(2x+3)(2x+2)]\\35[x^2+3x+2x+6+x^2-x]=17[4x^2+4x+6x+6]\\35[2x^2+4x+6]=17[4x^2+10x+6]\\70x^2+140x+210=68x^2+170x+102\\70x^2-68x^2+140x-170x+210-102=0\\2x^2-30x+108=0`

Factorizing, we have:

`2(x-6)(x-9)=0\\x-6=0$ or $x-9=0\\x=6$ or 9`

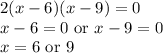
Therefore, the two different numbers of green pens that could be in the box are 6 or 9.