Question

The half-wave rectifier below is operating at a frequency of 60 Hz, and the rms value of the transformer output voltage is 6.3 V. (a) What is the value of the dc output voltage VO if the diode voltage drop is 1 V? (b) What is the minimum value of C required to maintain the ripple voltage to less than 0.25 V if R = 0.5Ω?

Answer 1

Given Information:

Frequency = f = 60 Hz

Transformer output voltage = Vrms = 6.3 V

Diode voltage drop = Vd = 1 V

Ripper voltage = Vr = 0.25 V

Load resistance = R = 0.5 Ω

Required Information:

a) dc output voltage = V₀ = ?

b) Capacitane = C = ?

Answer:

a) dc output voltage = V₀ = 2.52 V

b) Capacitane = C = 0.336 F

Step-by-step explanation:

a) The average or dc output voltage of a half-wave rectifier is given by

`V_0 = V_p/\pi`

Where Vp is given by

`V_p = (V_(rms) * √(2)) - V_d \\\\V_p = (6.3 * √(2)) - 1 \\\\V_p = 8.91 - 1 \\\\V_p = 7.91 \: V \\\\`

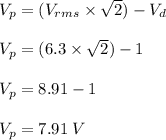
So, the dc output voltage is

`V_0 = 7.91/\pi \\\\V_0 = 2.52 \: V`

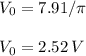
b) The minimum value of C required to maintain the ripple voltage to less than 0.25 V is given by

`$ C = (I)/(Vr \cdot f) $`

Where I is current, Vr is the ripple voltage and f is the frequency

`$ I = (V_0)/(R) $`

`$ I = (2.52)/(0.5) $`

`I = 5.04 \: A`

`$ C = (5.04)/(0.25 \cdot 60) $`

`C = 0.336 \: F`

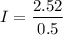
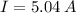
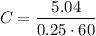
Therefore, 0.336 F is the minimum value of capacitance required to maintain the ripple voltage to less than 0.25 V