Question

Prove ABCD is a parallelogram by showing both pairs of opposite sides are parallel. please Show All Work! Thanks!!

Answer 1

Here You Go! I'm not really sure about this one but i tried.

Explanation:

Answer 2

Explanation:

To prove this we should first make a little representation to get an idea of how will proceed to work .

To solve it we should use vectors so the first step is to identify this vectors :

• we have four points : A/B/C/D

1. A(-2,-4)
2. B(1,2)
3. C(2,10)
4. D(-1,4)

• VECTOR AB WITH VECTOR DC
• VECTOR AD WITH VECTOR BC

NOW LET'S IDENTIFY THEIR COORDINATES :

• VECTOR AB (1-(-2),2-(-4)) VECTOR DC (2-(-1),10-4)
• VECTOR AD (-1-(-2),4-(-4)) VECTOR BC (2-1,10-2)

We get :

• VECTOR AB (3,6) VECTOR DC (3,6)
• VECTOR AD (1,8) VECTOR BC (1,8)

We notice that the opposite ones have the same coordinates so the edges are parallel .

If we want to check more we can calculate the lenghts :

• AB=
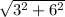  `\sqrt{3^(2)+6^(2) }` DC=
  `\sqrt{3^(2)+6^(2) }`

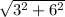
So AB=DC

• AD=
  `\sqrt{1^(2)+8^(2) }` BC=
  `\sqrt{1^(2)+8^(2) }`

So AD=BC

SO ABCD IS A PARALLELOGRAM