Question

Recall the equation for a circle with center (h,k) and radius r. At what point in the first quadrant does the line with equation y=2x+5 intersect the circle with radius 5 and center (0, 5)?

Answer 1

(2.236,9.472).

Explanation:

The standard form of a circle is

`(x-h)^2+(y-k)^2=r^2` ...(1)

where, (h,k) is center and r is radius of the circle.

It is given that radius of the circle is 5 and center at (0,5). So, the equation of circle is

`(x-0)^2+(y-5)^2=5^2`

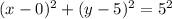
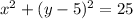`x^2+(y-5)^2=25` ...(2)

The given equation of line is

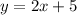`y=2x+5` ...(3)

We need to find the intersection point of line and circle in first quadrant.

On solving (2) and (3), we get

`x^2+((2x+5)-5)^2=25`

`x^2+(2x)^2=25`

`x^2+4x^2=25`

`5x^2=25`

`x^2=5`

`x=\pm √(5)=\pm 2.236`

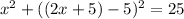
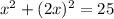
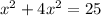
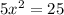
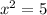
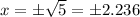
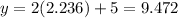
At x=2.236,

`y=2(2.236)+5=9.472`

At x=-2.236,

`y=2(-2.236)+5=0.528`

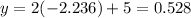
It means line intersect the circle at (2.236,9.472) and (-2.236,0.528).

In first quadrant both coordinates are positive.

Therefore, the required point is (2.236,9.472).